Coastal flooding models based on the numerical solution of the 2D shallow water equations are used widely to predict the timing and magnitude of inundation during storms, both in real-time forecasting and long-term design. Constraints on computing time, especially in forecasting, can limit the models’ spatial resolution and hence their accuracy. However, it is desirable to have fast flooding predictions that also include the best-available representation of flow pathways and barriers at the scales of critical infrastructure. This need can be addressed via subgrid corrections, which use information at smaller scales to ‘correct’ the flow variables (water levels and current velocities) averaged over the model scale.
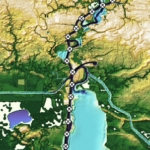 In this dissertation, subgrid corrections have been added to the ADvanced CIRCulation (ADCIRC) model, a widely used, continuous-Galerkin finite-element based, shallow water flow model. This includes the full derivation of averaged governing equations, closure approximations, and subgrid implementation into the source code. Testing of this new model was first performed on 3 domains: an idealized winding channel, a tidally influenced bay in Massachusetts, and a regional storm surge model covering Calcasieu Lake in Southwestern Louisiana with forcing from Rita (2005). By pre-computing the averaged variables from high-resolution bathy/topo data sets, the model can represent hydraulic connectivity at smaller scales. This allows for a coarsening of the model and thus faster predictions of flooding, while also improving accuracy. The implementation permits changing a logic-based wetting and drying algorithm to a more desirable logic-less algorithm, and requires averaging correction factors on both an elemental and vertex basis. This new framework further increases efficiency of the model, and is general enough to be used in other Galerkin-based, finite-element, hydrodynamic models. It is shown that the flooding model with subgrid corrections can match the accuracy of the conventional model, while offering a 10 to 50 times increase in speed.
In this dissertation, subgrid corrections have been added to the ADvanced CIRCulation (ADCIRC) model, a widely used, continuous-Galerkin finite-element based, shallow water flow model. This includes the full derivation of averaged governing equations, closure approximations, and subgrid implementation into the source code. Testing of this new model was first performed on 3 domains: an idealized winding channel, a tidally influenced bay in Massachusetts, and a regional storm surge model covering Calcasieu Lake in Southwestern Louisiana with forcing from Rita (2005). By pre-computing the averaged variables from high-resolution bathy/topo data sets, the model can represent hydraulic connectivity at smaller scales. This allows for a coarsening of the model and thus faster predictions of flooding, while also improving accuracy. The implementation permits changing a logic-based wetting and drying algorithm to a more desirable logic-less algorithm, and requires averaging correction factors on both an elemental and vertex basis. This new framework further increases efficiency of the model, and is general enough to be used in other Galerkin-based, finite-element, hydrodynamic models. It is shown that the flooding model with subgrid corrections can match the accuracy of the conventional model, while offering a 10 to 50 times increase in speed.
 Next, higher level corrections to bottom friction and advection were incorporated into the subgrid model, and the framework was expanded and tested at the ocean-scale. It was hypothesized that by adding higher-level corrections to the model and applying them to ocean-scale domains, accurate predictions of storm surge at the smallest coastal scales can be obtained. To accomplish this, higher-level corrections were derived and implemented into the governing equations and extensive elevation and landcover data sets were curated to cover the South Atlantic Bight region of the U.S. Atlantic Coast. From there, the subgrid model was tested on an ocean-scale domain with tidal and meteorological forcing from Matthew (2016). The improvements in water level prediction accuracy due to subgrid corrections are evaluated at 218 observation locations throughout 1500 km of coast along the South Atlantic Bight. The accuracy of the subgrid model with relatively coarse spatial resolution (RMSE = 0.41 m) is better than that of a conventional model with relatively fine spatial resolution (RMSE = 0.67 m).By running on the coarsened subgrid model, we improved the accuracy over efficiency curve for the model, and as a result the computational expense of the simulation was decreased by a factor of 13.
Next, higher level corrections to bottom friction and advection were incorporated into the subgrid model, and the framework was expanded and tested at the ocean-scale. It was hypothesized that by adding higher-level corrections to the model and applying them to ocean-scale domains, accurate predictions of storm surge at the smallest coastal scales can be obtained. To accomplish this, higher-level corrections were derived and implemented into the governing equations and extensive elevation and landcover data sets were curated to cover the South Atlantic Bight region of the U.S. Atlantic Coast. From there, the subgrid model was tested on an ocean-scale domain with tidal and meteorological forcing from Matthew (2016). The improvements in water level prediction accuracy due to subgrid corrections are evaluated at 218 observation locations throughout 1500 km of coast along the South Atlantic Bight. The accuracy of the subgrid model with relatively coarse spatial resolution (RMSE = 0.41 m) is better than that of a conventional model with relatively fine spatial resolution (RMSE = 0.67 m).By running on the coarsened subgrid model, we improved the accuracy over efficiency curve for the model, and as a result the computational expense of the simulation was decreased by a factor of 13.
 Finally, subgrid corrections were systematically tested on a series of five ocean-scale meshes with minimum nearshore resolutions ranging from around 60 m on the highest resolution mesh to 1000 m on the coarsest mesh. This study aimed to find the mesh resolution that offered the best trade-off between accuracy and efficiency. The limitations of the subgrid model were explored and guidelines for future users were established. In all, it was found that the primary limitation to the subgrid model came from the aliasing of important flow-blocking features such as barrier islands in the coarsest resolution meshes. However, in areas without these features subgrid corrections can offer tremendous advantages while running on very coarse meshes.
Finally, subgrid corrections were systematically tested on a series of five ocean-scale meshes with minimum nearshore resolutions ranging from around 60 m on the highest resolution mesh to 1000 m on the coarsest mesh. This study aimed to find the mesh resolution that offered the best trade-off between accuracy and efficiency. The limitations of the subgrid model were explored and guidelines for future users were established. In all, it was found that the primary limitation to the subgrid model came from the aliasing of important flow-blocking features such as barrier islands in the coarsest resolution meshes. However, in areas without these features subgrid corrections can offer tremendous advantages while running on very coarse meshes.
The work completed in this dissertation moves the science of subgrid corrections forward by integrating the corrections into a widely used ocean-circulation and storm surge model. This work offers improvements to both hurricane storm surge forecasting and long-term design by allowing for reduced run-times and increased accuracy on coarsened numerical meshes.
JL Woodruff (2023). “Subgrid Corrections in Storm-Driven Coastal Flooding,” North Carolina State University.
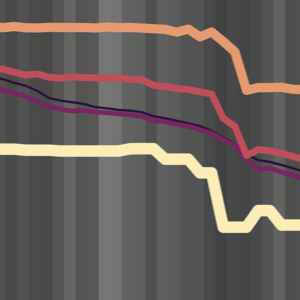 Flooding due to storm surge can propagate through coastal regions to threaten the built and natural environments. This propagation is controlled by geographic features of varying scales, from the largest oceans to the smallest marsh channels and sandy dunes. Numerical models to predict coastal flooding have been improved via the use of subgrid corrections, which use information about the smallest-scale flow controls to provide corrections to coarser scale grids. Although previous studies have demonstrated the benefits of subgrid models, especially how coarser models can be more efficient without a trade-off in accuracy, this study systematically investigates subgrid corrections in storm surge models across large domains. Here, we apply the widely used ADVanced CIRCulation (ADCIRC) storm surge model with revised subgrid corrections to develop guidance for resolution of coastal regions. Recent hurricanes in the South Atlantic Bight are simulated with five models, each with varying resolution of coastal islands, estuaries, rivers, and floodplains. Model performance is quantified via comparisons with observed data and high-resolution simulations. Clear degradation is observed in the subgrid model performance as minimum mesh resolution becomes coarser than the width of channels conveying flow or the barrier islands blocking flow. Therefore, subgrid model mesh resolution should account for spatial scales of local flow pathways and barrier islands to maintain proper model mass and momentum transfer. However, with subgrid modeling this can be done at much coarser (and thus computationally faster) resolutions than with conventional models.
Flooding due to storm surge can propagate through coastal regions to threaten the built and natural environments. This propagation is controlled by geographic features of varying scales, from the largest oceans to the smallest marsh channels and sandy dunes. Numerical models to predict coastal flooding have been improved via the use of subgrid corrections, which use information about the smallest-scale flow controls to provide corrections to coarser scale grids. Although previous studies have demonstrated the benefits of subgrid models, especially how coarser models can be more efficient without a trade-off in accuracy, this study systematically investigates subgrid corrections in storm surge models across large domains. Here, we apply the widely used ADVanced CIRCulation (ADCIRC) storm surge model with revised subgrid corrections to develop guidance for resolution of coastal regions. Recent hurricanes in the South Atlantic Bight are simulated with five models, each with varying resolution of coastal islands, estuaries, rivers, and floodplains. Model performance is quantified via comparisons with observed data and high-resolution simulations. Clear degradation is observed in the subgrid model performance as minimum mesh resolution becomes coarser than the width of channels conveying flow or the barrier islands blocking flow. Therefore, subgrid model mesh resolution should account for spatial scales of local flow pathways and barrier islands to maintain proper model mass and momentum transfer. However, with subgrid modeling this can be done at much coarser (and thus computationally faster) resolutions than with conventional models.
 Flooding due to storm surge can propagate through coastal regions to threaten the built and natural environments. This propagation is controlled by geographic features of varying scales, from the largest oceans to the smallest marsh channels and sandy dunes. Numerical models to predict coastal flooding have been improved via the use of subgrid corrections, which use information about the smallest-scale flow controls to provide corrections to coarser scale grids. Although previous studies have demonstrated the benefits of subgrid models, especially how coarser models can be more efficient without a trade-off in accuracy, this study systematically investigates subgrid corrections in storm surge models across large domains. Here, we apply the widely used ADVanced CIRCulation (ADCIRC) storm surge model with revised subgrid corrections to develop guidance for resolution of coastal regions. Recent hurricanes in the South Atlantic Bight are simulated with five models, each with varying resolution of coastal islands, estuaries, rivers, and floodplains. Model performance is quantified via comparisons with observed data and high-resolution simulations. Clear degradation is observed in the subgrid model performance as minimum mesh resolution becomes coarser than the width of channels conveying flow or the barrier islands blocking flow. Therefore, subgrid model mesh resolution should account for spatial scales of local flow pathways and barrier islands to maintain proper model mass and momentum transfer. However, with subgrid modeling this can be done at much coarser (and thus computationally faster) resolutions than with conventional models.
Flooding due to storm surge can propagate through coastal regions to threaten the built and natural environments. This propagation is controlled by geographic features of varying scales, from the largest oceans to the smallest marsh channels and sandy dunes. Numerical models to predict coastal flooding have been improved via the use of subgrid corrections, which use information about the smallest-scale flow controls to provide corrections to coarser scale grids. Although previous studies have demonstrated the benefits of subgrid models, especially how coarser models can be more efficient without a trade-off in accuracy, this study systematically investigates subgrid corrections in storm surge models across large domains. Here, we apply the widely used ADVanced CIRCulation (ADCIRC) storm surge model with revised subgrid corrections to develop guidance for resolution of coastal regions. Recent hurricanes in the South Atlantic Bight are simulated with five models, each with varying resolution of coastal islands, estuaries, rivers, and floodplains. Model performance is quantified via comparisons with observed data and high-resolution simulations. Clear degradation is observed in the subgrid model performance as minimum mesh resolution becomes coarser than the width of channels conveying flow or the barrier islands blocking flow. Therefore, subgrid model mesh resolution should account for spatial scales of local flow pathways and barrier islands to maintain proper model mass and momentum transfer. However, with subgrid modeling this can be done at much coarser (and thus computationally faster) resolutions than with conventional models.

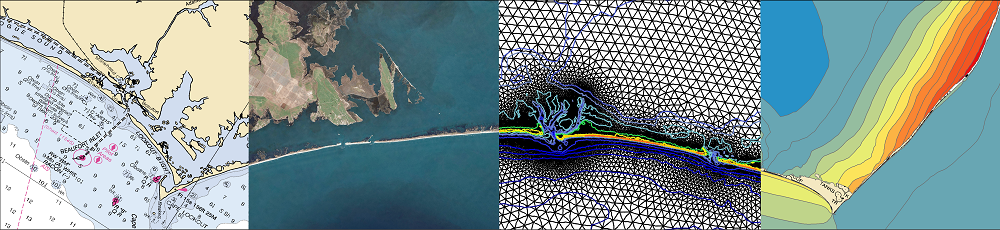

 In this dissertation, subgrid corrections have been added to the ADvanced CIRCulation (ADCIRC) model, a widely used, continuous-Galerkin finite-element based, shallow water flow model. This includes the full derivation of averaged governing equations, closure approximations, and subgrid implementation into the source code. Testing of this new model was first performed on 3 domains: an idealized winding channel, a tidally influenced bay in Massachusetts, and a regional storm surge model covering Calcasieu Lake in Southwestern Louisiana with forcing from Rita (2005). By pre-computing the averaged variables from high-resolution bathy/topo data sets, the model can represent hydraulic connectivity at smaller scales. This allows for a coarsening of the model and thus faster predictions of flooding, while also improving accuracy. The implementation permits changing a logic-based wetting and drying algorithm to a more desirable logic-less algorithm, and requires averaging correction factors on both an elemental and vertex basis. This new framework further increases efficiency of the model, and is general enough to be used in other Galerkin-based, finite-element, hydrodynamic models. It is shown that the flooding model with subgrid corrections can match the accuracy of the conventional model, while offering a 10 to 50 times increase in speed.
In this dissertation, subgrid corrections have been added to the ADvanced CIRCulation (ADCIRC) model, a widely used, continuous-Galerkin finite-element based, shallow water flow model. This includes the full derivation of averaged governing equations, closure approximations, and subgrid implementation into the source code. Testing of this new model was first performed on 3 domains: an idealized winding channel, a tidally influenced bay in Massachusetts, and a regional storm surge model covering Calcasieu Lake in Southwestern Louisiana with forcing from Rita (2005). By pre-computing the averaged variables from high-resolution bathy/topo data sets, the model can represent hydraulic connectivity at smaller scales. This allows for a coarsening of the model and thus faster predictions of flooding, while also improving accuracy. The implementation permits changing a logic-based wetting and drying algorithm to a more desirable logic-less algorithm, and requires averaging correction factors on both an elemental and vertex basis. This new framework further increases efficiency of the model, and is general enough to be used in other Galerkin-based, finite-element, hydrodynamic models. It is shown that the flooding model with subgrid corrections can match the accuracy of the conventional model, while offering a 10 to 50 times increase in speed. Next, higher level corrections to bottom friction and advection were incorporated into the subgrid model, and the framework was expanded and tested at the ocean-scale. It was hypothesized that by adding higher-level corrections to the model and applying them to ocean-scale domains, accurate predictions of storm surge at the smallest coastal scales can be obtained. To accomplish this, higher-level corrections were derived and implemented into the governing equations and extensive elevation and landcover data sets were curated to cover the South Atlantic Bight region of the U.S. Atlantic Coast. From there, the subgrid model was tested on an ocean-scale domain with tidal and meteorological forcing from Matthew (2016). The improvements in water level prediction accuracy due to subgrid corrections are evaluated at 218 observation locations throughout 1500 km of coast along the South Atlantic Bight. The accuracy of the subgrid model with relatively coarse spatial resolution (RMSE = 0.41 m) is better than that of a conventional model with relatively fine spatial resolution (RMSE = 0.67 m).By running on the coarsened subgrid model, we improved the accuracy over efficiency curve for the model, and as a result the computational expense of the simulation was decreased by a factor of 13.
Next, higher level corrections to bottom friction and advection were incorporated into the subgrid model, and the framework was expanded and tested at the ocean-scale. It was hypothesized that by adding higher-level corrections to the model and applying them to ocean-scale domains, accurate predictions of storm surge at the smallest coastal scales can be obtained. To accomplish this, higher-level corrections were derived and implemented into the governing equations and extensive elevation and landcover data sets were curated to cover the South Atlantic Bight region of the U.S. Atlantic Coast. From there, the subgrid model was tested on an ocean-scale domain with tidal and meteorological forcing from Matthew (2016). The improvements in water level prediction accuracy due to subgrid corrections are evaluated at 218 observation locations throughout 1500 km of coast along the South Atlantic Bight. The accuracy of the subgrid model with relatively coarse spatial resolution (RMSE = 0.41 m) is better than that of a conventional model with relatively fine spatial resolution (RMSE = 0.67 m).By running on the coarsened subgrid model, we improved the accuracy over efficiency curve for the model, and as a result the computational expense of the simulation was decreased by a factor of 13. Finally, subgrid corrections were systematically tested on a series of five ocean-scale meshes with minimum nearshore resolutions ranging from around 60 m on the highest resolution mesh to 1000 m on the coarsest mesh. This study aimed to find the mesh resolution that offered the best trade-off between accuracy and efficiency. The limitations of the subgrid model were explored and guidelines for future users were established. In all, it was found that the primary limitation to the subgrid model came from the aliasing of important flow-blocking features such as barrier islands in the coarsest resolution meshes. However, in areas without these features subgrid corrections can offer tremendous advantages while running on very coarse meshes.
Finally, subgrid corrections were systematically tested on a series of five ocean-scale meshes with minimum nearshore resolutions ranging from around 60 m on the highest resolution mesh to 1000 m on the coarsest mesh. This study aimed to find the mesh resolution that offered the best trade-off between accuracy and efficiency. The limitations of the subgrid model were explored and guidelines for future users were established. In all, it was found that the primary limitation to the subgrid model came from the aliasing of important flow-blocking features such as barrier islands in the coarsest resolution meshes. However, in areas without these features subgrid corrections can offer tremendous advantages while running on very coarse meshes.
 Inundation models represent coastal regions with a grid of computational points, often with varying resolution of flow pathways and barriers. Models based on coarse grid solutions of shallow water equations have been improved recently via the use of subgrid corrections, which account for information (ground surface elevations, roughness characteristics) at smaller scales. In this work, numerical approaches of an established storm surge model are extended to include subgrid corrections. In an attempt to maintain continuity with existing users and results, model extensions were limited to those needed to provide basic subgrid capabilities, and included two major additions. First, a finite volume method is used to incorporate corrections to the mass and momentum equations using high-resolution ground surface elevations. Second, the no-slip condition imposed on the B-grid wet/dry interface in the model is modified to a slip condition to enable flows in channels with widths comparable to cell size. Numerical results demonstrate these numerical extensions can significantly enhance the accuracy of the model’s predictions of coastal flooding, with low additional computational cost.
Inundation models represent coastal regions with a grid of computational points, often with varying resolution of flow pathways and barriers. Models based on coarse grid solutions of shallow water equations have been improved recently via the use of subgrid corrections, which account for information (ground surface elevations, roughness characteristics) at smaller scales. In this work, numerical approaches of an established storm surge model are extended to include subgrid corrections. In an attempt to maintain continuity with existing users and results, model extensions were limited to those needed to provide basic subgrid capabilities, and included two major additions. First, a finite volume method is used to incorporate corrections to the mass and momentum equations using high-resolution ground surface elevations. Second, the no-slip condition imposed on the B-grid wet/dry interface in the model is modified to a slip condition to enable flows in channels with widths comparable to cell size. Numerical results demonstrate these numerical extensions can significantly enhance the accuracy of the model’s predictions of coastal flooding, with low additional computational cost.