
A number of finite-element based shallow water models use the GWC (generalized wave continuity) algorithm, first introduced by Lynch and Gray in 1979, to suppress short wave noise without artificial or numerical damping. Nearly all of these, including the ADCIRC (ADvanced 3D CIRCulation model developed by Westerink and Luettich) model used in our research, utilize the non-conservative form of the momentum equation to obtain the velocity field. However, as early as 1990, it was discovered that the inconsistent treatment of the advective terms between the GWC equation (which uses the conservative form of the momentum equation in its formulation) and the non-conservative momentum (NCM) equation was causing instabilities. Additional analyses by Kinnmark and Aldama, among others, provided further evidence that the conservative form of the momentum (CM) equation may improve accuracy and stability, particularly for simulations that have regions of highly advective flows, e.g., converging flow near inlets and around barrier islands. Furthermore, as the ADCIRC modeling group begins to explore alternative algorithms for the continuity equations (e.g., discontinuous Galerkin algorithm instead of GWC), the conservative form of the momentum equation would facilitate model coupling. For these reasons, we modified the ADCIRC code to use the conservative form of the momentum equation. The impact of this change on mass balance, stability, and accuracy (spatial and temporal) is rigorously assessed, first for ID barotropic flows and later for 2D barotropic flows in a variety of basins. Results from the 1D experiments indicate the following: global mass balance improves up to two orders of magnitude, depending on the domain; local mass balance greatly improves in areas where steep bathymetry gradients occur; when combined with a predictor-corrector time-marching algorithm, stability increases by at least a factor of two (for a given level of mass balance error); and the form of the momentum equation does not cause a significant change in temporal or spatial accuracy when evaluating the two different time-marching algorithms.
KM Dresback, RL Kolar, JC Dietrich (2002). “Impact of the Form of the Momentum Equation on Shallow Water Models based on the Generalized Wave Continuity Equation.” Proceedings of the XIV International Conference on Computational Methods in Water Resources (CMWR), SM Hassanizadeh, RJ Schotting, WG Gray, and GF Pinder, eds., 47, 1573-1580.
 As sea levels continue to rise, coastal communities are searching for strategies to reduce flooding of low-lying roads, property, and stormwater drainage networks. Here we focus on the development of adaptation strategies for communities that experience flooding outside of extreme storms like hurricanes due to sea level rise (SLR). Processes that contribute to these floods can include tides, rainfall, wind setup, groundwater, and infrastructure failure (Gold et al., 2023). Here we present a framework to test the effectiveness of adaptation strategies in reducing multi-driver chronic flooding at both current and future sea levels. This framework integrates coastal engineering and stakeholder input to 1) identify adaptation strategies that are preferred by a community that frequently floods and 2) test the effectiveness of these strategies with a numerical model under both current and future conditions.
As sea levels continue to rise, coastal communities are searching for strategies to reduce flooding of low-lying roads, property, and stormwater drainage networks. Here we focus on the development of adaptation strategies for communities that experience flooding outside of extreme storms like hurricanes due to sea level rise (SLR). Processes that contribute to these floods can include tides, rainfall, wind setup, groundwater, and infrastructure failure (Gold et al., 2023). Here we present a framework to test the effectiveness of adaptation strategies in reducing multi-driver chronic flooding at both current and future sea levels. This framework integrates coastal engineering and stakeholder input to 1) identify adaptation strategies that are preferred by a community that frequently floods and 2) test the effectiveness of these strategies with a numerical model under both current and future conditions.
 As sea levels continue to rise, coastal communities are searching for strategies to reduce flooding of low-lying roads, property, and stormwater drainage networks. Here we focus on the development of adaptation strategies for communities that experience flooding outside of extreme storms like hurricanes due to sea level rise (SLR). Processes that contribute to these floods can include tides, rainfall, wind setup, groundwater, and infrastructure failure (Gold et al., 2023). Here we present a framework to test the effectiveness of adaptation strategies in reducing multi-driver chronic flooding at both current and future sea levels. This framework integrates coastal engineering and stakeholder input to 1) identify adaptation strategies that are preferred by a community that frequently floods and 2) test the effectiveness of these strategies with a numerical model under both current and future conditions.
As sea levels continue to rise, coastal communities are searching for strategies to reduce flooding of low-lying roads, property, and stormwater drainage networks. Here we focus on the development of adaptation strategies for communities that experience flooding outside of extreme storms like hurricanes due to sea level rise (SLR). Processes that contribute to these floods can include tides, rainfall, wind setup, groundwater, and infrastructure failure (Gold et al., 2023). Here we present a framework to test the effectiveness of adaptation strategies in reducing multi-driver chronic flooding at both current and future sea levels. This framework integrates coastal engineering and stakeholder input to 1) identify adaptation strategies that are preferred by a community that frequently floods and 2) test the effectiveness of these strategies with a numerical model under both current and future conditions.

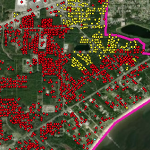 Hurricanes or typhoons are multi-hazard events that usually result in strong winds, storm surge, waves, and debris flow. A community-level multi-hazard hurricane risk analysis approach is proposed herein to account for the combined impacts of hazards driven by hurricanes including surge, wave, and wind. A tightly coupled ADCIRC and SWAN model is used to account for the surge and wave hazard. Community-level exposure analysis is conducted using a portfolio of building archetypes associated with each hazard. A building-level hurricane vulnerability model is developed using fragility functions to account for content, building envelope, and structural damage. These fragility functions calculate the exceedance probability of predefined damage states associated with each hazard. Then, a building damage state is calculated based on the maximum probability of being in each damage state corresponding to each hazard. The proposed hurricane risk model is then applied to Waveland, Mississippi, a community that was severely impacted by Hurricane Katrina in 2005. The main contribution of this research is modeling the community-level hurricane vulnerability in terms of damage to the building envelope and interior contents driven by surge, wave, and wind using fragility functions to provide a comprehensive model for resilience-informed decision-making.
Hurricanes or typhoons are multi-hazard events that usually result in strong winds, storm surge, waves, and debris flow. A community-level multi-hazard hurricane risk analysis approach is proposed herein to account for the combined impacts of hazards driven by hurricanes including surge, wave, and wind. A tightly coupled ADCIRC and SWAN model is used to account for the surge and wave hazard. Community-level exposure analysis is conducted using a portfolio of building archetypes associated with each hazard. A building-level hurricane vulnerability model is developed using fragility functions to account for content, building envelope, and structural damage. These fragility functions calculate the exceedance probability of predefined damage states associated with each hazard. Then, a building damage state is calculated based on the maximum probability of being in each damage state corresponding to each hazard. The proposed hurricane risk model is then applied to Waveland, Mississippi, a community that was severely impacted by Hurricane Katrina in 2005. The main contribution of this research is modeling the community-level hurricane vulnerability in terms of damage to the building envelope and interior contents driven by surge, wave, and wind using fragility functions to provide a comprehensive model for resilience-informed decision-making.
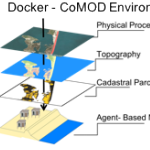 Tackling critical questions often requires the collaboration of researchers from different disciplines or institutions. Coastal hazards research is necessarily interdisciplinary and multi- methodological and often requires a team of researchers, due to its combination of storm-induced changes to the coastal environment, the effects of these changes on built infrastructure, and the combined effects on decision-making for individuals and communities. This paper introduces an interdisciplinary coastal hazard risk model that combines high resolution geospatial data, storm impact forecasts, and an agent-based model in the analysis, and then describes the model’s implementation in a data science cyberinfrastructure. Lessons learned and limitations are also outlined.
Tackling critical questions often requires the collaboration of researchers from different disciplines or institutions. Coastal hazards research is necessarily interdisciplinary and multi- methodological and often requires a team of researchers, due to its combination of storm-induced changes to the coastal environment, the effects of these changes on built infrastructure, and the combined effects on decision-making for individuals and communities. This paper introduces an interdisciplinary coastal hazard risk model that combines high resolution geospatial data, storm impact forecasts, and an agent-based model in the analysis, and then describes the model’s implementation in a data science cyberinfrastructure. Lessons learned and limitations are also outlined.
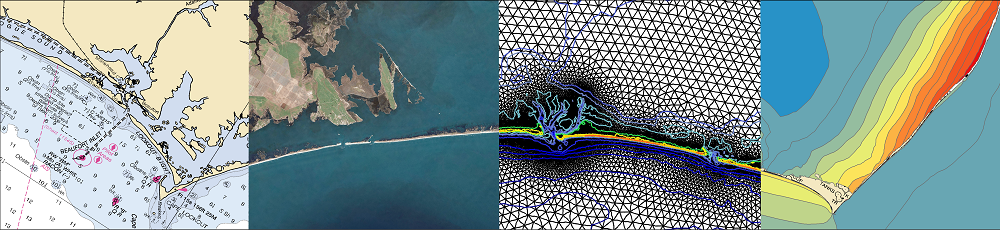
 Few wave measurements have been made in wetlands during high-energy, surge events, such as hurricanes. During Hurricane Gustav in 2008, many nearshore wave measurements were made in Southeastern Louisiana. These data are used to verify a nearshore wave modeling system and to explore the characteristics of hurricane waves in wetlands. The modeling system consists of the wave generation model WAM, the nearhsore wave model STWAVE, and the circulation model ADCIRC. The measurements confirm reasonable success in modeling the waves. The measurements and modeling also expose some of the problems of measuring waves in highly-variable water depths under hurricane forcing and modeling waves in rapidly degrading wetlands.
Few wave measurements have been made in wetlands during high-energy, surge events, such as hurricanes. During Hurricane Gustav in 2008, many nearshore wave measurements were made in Southeastern Louisiana. These data are used to verify a nearshore wave modeling system and to explore the characteristics of hurricane waves in wetlands. The modeling system consists of the wave generation model WAM, the nearhsore wave model STWAVE, and the circulation model ADCIRC. The measurements confirm reasonable success in modeling the waves. The measurements and modeling also expose some of the problems of measuring waves in highly-variable water depths under hurricane forcing and modeling waves in rapidly degrading wetlands.
 This paper provides a brief overview of several ongoing modeling projects that seek to predict the impact of physical features on hurricane storm surge and waves along the Louisiana Gulf Coast. All of the modeling projects described herein make use of a coupled ADCIRC/STWAVE computer model that is being developed specifically for capturing the inundation dynamics of Southern Louisiana. The projects also make use of a common statistical framework and a suite of 152 synthetic hurricane wind and pressure fields that have been developed to represent the storm dynamics along this region of the coast. This paper provides an overview of the statistical method, the computer models being applied, the physical features resolved by the finite element mesh, the validation exercises, the process for coupling and running the ADCIRC/STWAVE model, and a description of several investigations for which the coupled modeling system is being applied. Preliminary results and conclusions are presented.
This paper provides a brief overview of several ongoing modeling projects that seek to predict the impact of physical features on hurricane storm surge and waves along the Louisiana Gulf Coast. All of the modeling projects described herein make use of a coupled ADCIRC/STWAVE computer model that is being developed specifically for capturing the inundation dynamics of Southern Louisiana. The projects also make use of a common statistical framework and a suite of 152 synthetic hurricane wind and pressure fields that have been developed to represent the storm dynamics along this region of the coast. This paper provides an overview of the statistical method, the computer models being applied, the physical features resolved by the finite element mesh, the validation exercises, the process for coupling and running the ADCIRC/STWAVE model, and a description of several investigations for which the coupled modeling system is being applied. Preliminary results and conclusions are presented.
 Coastal ocean hydrodynamic models are used to simulate water surface elevations and circulation in oceans, lakes, estuaries, rivers and floodplains. One such model is ADCIRC (ADvanced CIRCulation), which was originally developed more than 15 years ago and which is used for a variety of purposes, including naval fleet operations, storm surge predictions, and larvae transport. ADCIRC assumed fixed land boundaries until a wetting and drying algorithm was implemented in 1995. However, this algorithm had two components that limited the performance of the model. First, nodes were required to remain “wet” or “dry” for a user-specified number of time steps before changing states. This component became restrictive in relatively flat regions, such as a flood plain, where it caused oscillations and slowed the propagation of flood waves. Second, in regions with steep bathymetry, mass balance problems and instabilities would occur when a thin film of water was allowed to flow uninterrupted. Changes based on a more physically-accurate description of the wetting and drying process were made recently to address these two problems. This paper describes the wetting and drying algorithm and those changes, and it applies the improved algorithm to an idealized domain that was designed specifically to test the two problem areas. The improved algorithm provides better stability and mass balance properties.
Coastal ocean hydrodynamic models are used to simulate water surface elevations and circulation in oceans, lakes, estuaries, rivers and floodplains. One such model is ADCIRC (ADvanced CIRCulation), which was originally developed more than 15 years ago and which is used for a variety of purposes, including naval fleet operations, storm surge predictions, and larvae transport. ADCIRC assumed fixed land boundaries until a wetting and drying algorithm was implemented in 1995. However, this algorithm had two components that limited the performance of the model. First, nodes were required to remain “wet” or “dry” for a user-specified number of time steps before changing states. This component became restrictive in relatively flat regions, such as a flood plain, where it caused oscillations and slowed the propagation of flood waves. Second, in regions with steep bathymetry, mass balance problems and instabilities would occur when a thin film of water was allowed to flow uninterrupted. Changes based on a more physically-accurate description of the wetting and drying process were made recently to address these two problems. This paper describes the wetting and drying algorithm and those changes, and it applies the improved algorithm to an idealized domain that was designed specifically to test the two problem areas. The improved algorithm provides better stability and mass balance properties.
 The ADvanced CIRCulation (ADCIRC) model is a finite-element hydrodynamic model based on the generalized wave continuity equation (GWCE). The model assumed fixed land boundaries until a wetting and drying algorithm was implemented by Luettich and Westerink in 1995. The algorithm uses an element-based approach, effectively turning elements on and off based on water depths and a water level gradient. While robust in some simulations, the algorithm can be subject to instabilities in the solution during highly nonlinear events. Thus, a rigorous assessment of the algorithm’s stability, accuracy, mass balance properties, and parameter sensitivity under a variety of conditions is needed. Herein, we examine these issues using a one-dimensional implementation of the wetting and drying algorithm for basins with a linear slope; future studies will examine a wider variety of real and idealized basins. We believe the results of this work will benefit similar studies in two- or three-dimensions, for users and developers of both ADCIRC and other finite element models.
The ADvanced CIRCulation (ADCIRC) model is a finite-element hydrodynamic model based on the generalized wave continuity equation (GWCE). The model assumed fixed land boundaries until a wetting and drying algorithm was implemented by Luettich and Westerink in 1995. The algorithm uses an element-based approach, effectively turning elements on and off based on water depths and a water level gradient. While robust in some simulations, the algorithm can be subject to instabilities in the solution during highly nonlinear events. Thus, a rigorous assessment of the algorithm’s stability, accuracy, mass balance properties, and parameter sensitivity under a variety of conditions is needed. Herein, we examine these issues using a one-dimensional implementation of the wetting and drying algorithm for basins with a linear slope; future studies will examine a wider variety of real and idealized basins. We believe the results of this work will benefit similar studies in two- or three-dimensions, for users and developers of both ADCIRC and other finite element models.
 A number of finite-element based shallow water models use the GWC (generalized wave continuity) algorithm, first introduced by Lynch and Gray in 1979, to suppress short wave noise without artificial or numerical damping. Nearly all of these, including the ADCIRC (ADvanced 3D CIRCulation model developed by Westerink and Luettich) model used in our research, utilize the non-conservative form of the momentum equation to obtain the velocity field. However, as early as 1990, it was discovered that the inconsistent treatment of the advective terms between the GWC equation (which uses the conservative form of the momentum equation in its formulation) and the non-conservative momentum (NCM) equation was causing instabilities. Additional analyses by Kinnmark and Aldama, among others, provided further evidence that the conservative form of the momentum (CM) equation may improve accuracy and stability, particularly for simulations that have regions of highly advective flows, e.g., converging flow near inlets and around barrier islands. Furthermore, as the ADCIRC modeling group begins to explore alternative algorithms for the continuity equations (e.g., discontinuous Galerkin algorithm instead of GWC), the conservative form of the momentum equation would facilitate model coupling. For these reasons, we modified the ADCIRC code to use the conservative form of the momentum equation. The impact of this change on mass balance, stability, and accuracy (spatial and temporal) is rigorously assessed, first for ID barotropic flows and later for 2D barotropic flows in a variety of basins. Results from the 1D experiments indicate the following: global mass balance improves up to two orders of magnitude, depending on the domain; local mass balance greatly improves in areas where steep bathymetry gradients occur; when combined with a predictor-corrector time-marching algorithm, stability increases by at least a factor of two (for a given level of mass balance error); and the form of the momentum equation does not cause a significant change in temporal or spatial accuracy when evaluating the two different time-marching algorithms.
A number of finite-element based shallow water models use the GWC (generalized wave continuity) algorithm, first introduced by Lynch and Gray in 1979, to suppress short wave noise without artificial or numerical damping. Nearly all of these, including the ADCIRC (ADvanced 3D CIRCulation model developed by Westerink and Luettich) model used in our research, utilize the non-conservative form of the momentum equation to obtain the velocity field. However, as early as 1990, it was discovered that the inconsistent treatment of the advective terms between the GWC equation (which uses the conservative form of the momentum equation in its formulation) and the non-conservative momentum (NCM) equation was causing instabilities. Additional analyses by Kinnmark and Aldama, among others, provided further evidence that the conservative form of the momentum (CM) equation may improve accuracy and stability, particularly for simulations that have regions of highly advective flows, e.g., converging flow near inlets and around barrier islands. Furthermore, as the ADCIRC modeling group begins to explore alternative algorithms for the continuity equations (e.g., discontinuous Galerkin algorithm instead of GWC), the conservative form of the momentum equation would facilitate model coupling. For these reasons, we modified the ADCIRC code to use the conservative form of the momentum equation. The impact of this change on mass balance, stability, and accuracy (spatial and temporal) is rigorously assessed, first for ID barotropic flows and later for 2D barotropic flows in a variety of basins. Results from the 1D experiments indicate the following: global mass balance improves up to two orders of magnitude, depending on the domain; local mass balance greatly improves in areas where steep bathymetry gradients occur; when combined with a predictor-corrector time-marching algorithm, stability increases by at least a factor of two (for a given level of mass balance error); and the form of the momentum equation does not cause a significant change in temporal or spatial accuracy when evaluating the two different time-marching algorithms.