Tag Archives: Casey Dietrich
Wave Refraction on Coarse Meshes, Part 2
Updated 2016/07/31: This post is now outdated. SWAN has been updated to improve its treatment of the spectral propagation velocities, so these limiters are not needed. Please see this post.
Updated 2012/04/12: This is an old page. It persists on this site for posterity, but the information presented below is no longer up-to-date. When you are done here, then please click forward to this page, which describes how to control refraction errors with limiters on the spectral propagation velocities.
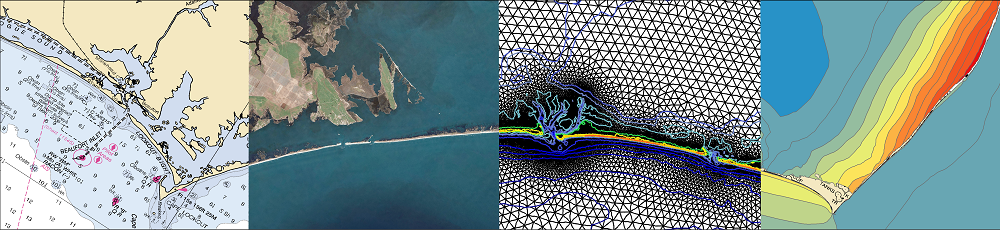
In a previous page on wave refraction, it was shown that mesh resolution plays an important role in how SWAN handles this physical process. If the mesh is resolved coarsely, then SWAN can refract too much energy, resulting in spikes in the wave solution. In our hurricane applications, we have observed spikes in the significant wave heights of 75m or larger, focused at only a few vertices, because the mesh in those regions does not resolve properly a shallow feature.
To address this problem, we added wave refraction as an attribute to the ADCIRC fort.13 file, so that it can be varied spatially. The user can enable refraction in regions with the necessary level of mesh resolution, and disable refraction in regions that are resolved coarsely. We enabled wave refraction along the northern Gulf coastline and within southern Louisiana, and we no longer saw the spikes in the significant wave heights in the regions offshore.
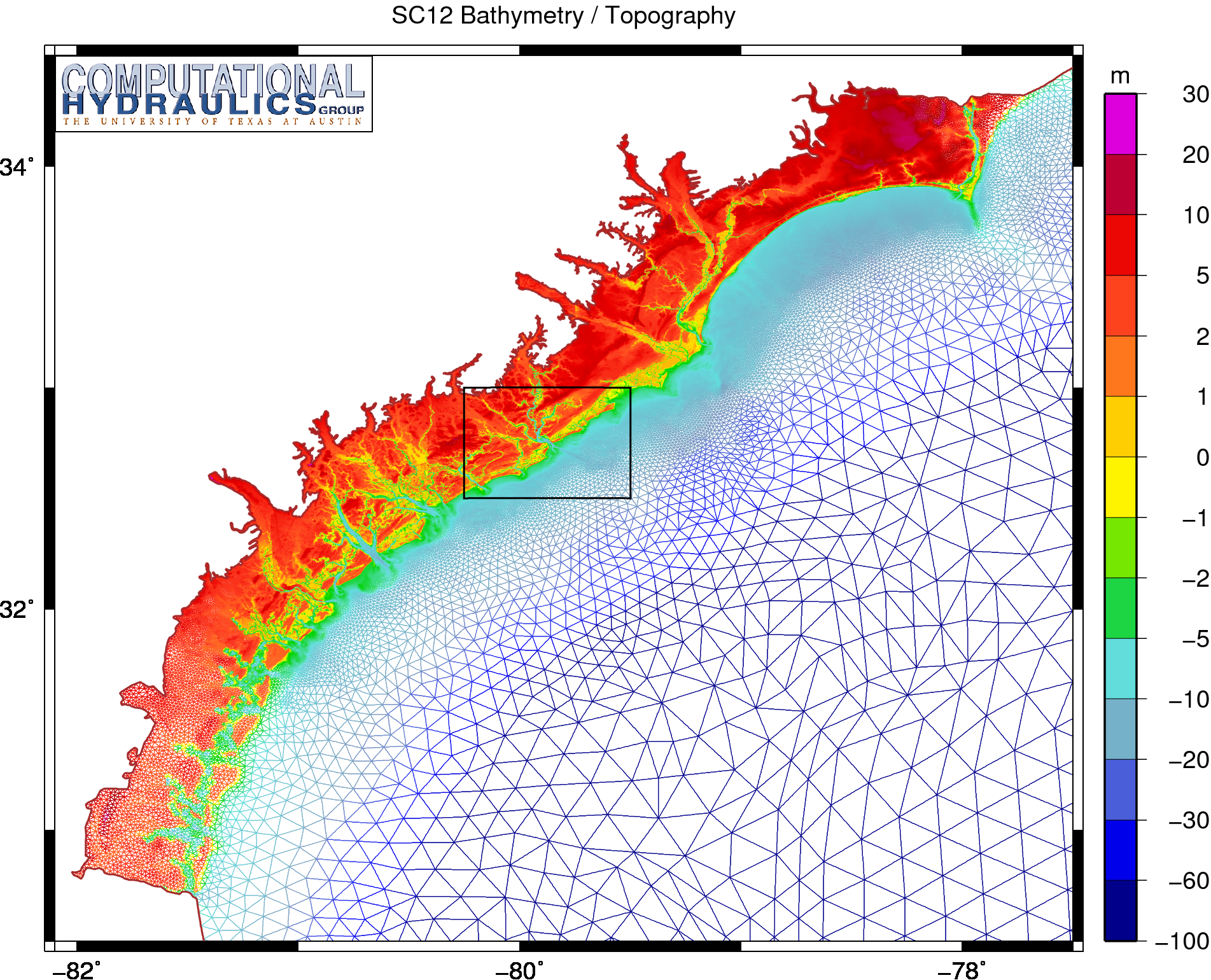
Bathymetry and topography (m) on the SC12 unstructured mesh.
Peak Periods TPS in South Carolina
However, we have learned recently that wave refraction on coarse meshes can be problematic in other ways besides creating spikes in the significant wave heights. For example, in very shallow regions, the dissipation of bottom friction and breaking would limit the significant wave heights to reasonable values, even if wave refraction was a problem. There would not be any spikes in the significant wave heights. But the focusing of wave energy would be apparent in other ways that are more subtle, such as the existence of peak periods with the maximum possible values.
On this page, we examine an instance of this problem with wave refraction on coase meshes. As a specific example, we consider a mesh that was developed for a flood inundation study along the coastline of South Carolina. It should be noted that, although this example mesh does exhibit these problems with wave refraction, the problems are also evident on other meshes and other applications. For example, we have seen similarly problematic peak periods in our hurricane applications in southern Louisiana. As we have noted previously, any wave model would face this problem of how to handle refraction on unstructured meshes.
Origin of the Hurricane Ike Forerunner Surge
A large, unpredicted, water level increase appeared along a substantial section of the western Louisiana and northern Texas (LATEX) coasts 12-24 hrs in advance of the landfall of Hurricane Ike (2008), with water levels in some areas reaching 3m above mean sea level. During this time the cyclonic wind field was largely shore parallel throughout the region. A similar early water level rise was reported for both the 1900 and the 1915 Galveston Hurricanes. The Ike forerunner anomaly occurred over a much larger area and prior to the primary coastal surge which was driven by onshore directed winds to the right of the storm track. We diagnose the forerunner surge as being generated by Ekman setup on the wide and shallow LATEX shelf. The longer forerunner time scale additionally served to increase water levels significantly in narrow-entranced coastal bays. The forerunner surge generated a freely propagating continental shelf wave with greater than 1.4m peak elevation that travelled coherently along the coast to Southern Texas, and was 300km in advance of the storm track at the time of landfall. This was, at some locations, the largest water level increase seen throughout the storm, and appears to be the largest freely-propagating shelf wave ever reported. Ekman setup-driven forerunners will be most significant on wide, shallow shelves subject to large wind fields, and need to be considered for planning and forecasting in these cases.
Conference: ADCIRC 2011
Conference: SIAM Geosciences 2011
JC Dietrich, CN Dawson, JD Meixner, JJ Westerink, AB Kennedy, RA Luettich Jr, EJ Kubatko, M Zijlema, LH Holthuijsen. “Performance of the Integrally – Coupled, Unstructured – Mesh SWAN + ADCIRC(DG) Model.” SIAM Conference on Mathematical and Computational Issues in the Geosciences, Long Beach, California, 21-24 March 2011.
JJ Westerink, JC Dietrich, CN Dawson, S Tanaka. “High Performance Scalable Computations of Hurricane Driven Wind Waves, Storm Surge, and Flow in Integrated Ocean Basin to Shelf to Inland Floodplain Systems.” SIAM Conference on Mathematical and Computational Issues in the Geosciences, Long Beach, California, 21-24 March 2011.
Seminar: Texas A&M University
Modeling Hurricane Waves and Storm Surge using Integrally-Coupled, Scalable Computations
The unstructured-mesh SWAN spectral wave model and the ADCIRC shallow-water circulation model have been integrated into a tightly-coupled SWAN+ADCIRC model. The model components are applied to an identical, unstructured mesh; share parallel computing infrastructure; and run sequentially in time. Wind speeds, water levels, currents and radiation stress gradients are vertex-based, and therefore can be passed through memory or cache to each model component. Parallel simulations based on domain decomposition utilize identical sub-meshes, and the communication is highly localized. Inter-model communication is intra-core, while intra-model communication is inter-core but is local and efficient because it is solely on adjacent sub-mesh edges. The resulting integrated SWAN+ADCIRC system is highly scalable and allows for localized increases in resolution without the complexity or cost of nested meshes or global interpolation between heterogeneous meshes. Hurricane waves and storm surge are validated for Hurricanes Katrina and Rita, demonstrating the importance of inclusion of the wave-circulation interactions, and efficient performance is demonstrated to 3062 computational cores.
Development and Application of Coupled Hurricane Wave and Surge Models for Southern Louisiana
Coastal Louisiana and Mississippi are especially prone to large hurricanes due to their geographic location in the north-central Gulf of Mexico. Several recent hurricanes have devastated the region, creating complicated environments of waves and storm surge. Katrina (2005) and Gustav (2008) made landfall in southeastern Louisiana, and their counter-clockwise winds pushed surge onto the Louisiana-Mississippi continental shelf, into the low-lying wetlands surrounding the Mississippi River, and over and through the levee system that protects metropolitan New Orleans. Rita (2005) and Ike (2008) passed farther to the west, moved across the Texas-Louisiana continental shelf, and created surge that flooded large portions of southwestern Louisiana.
These hurricanes demand detailed hindcasts that depict the evolution of waves and surge during these storm events. These hindcasts can be used to map the likely floodplains for insurance purposes, to understand how the current protection system responded during each storm, and to design a new protection system that will resist better the waves and surge. In addition, the resulting computational model can be used to forecast the system’s response to future storm events.
The work described herein represents a significant step forward in the modeling of hurricane waves and surge in complicated nearshore environments. The system is resolved with unprecedented levels of detail, including mesh sizes of 1km on the continental shelf, less than 200m in the wave breaking zones and inland, and down to 20-30m in the fine-scale rivers and channels. The resulting hindcasts are incredibly accurate, with close matches between the modeled results and the measured high-water marks and hydrograph data. They can be trusted to provide a faithful representation of the evolution of waves and surge during all four hurricanes.
This work also describes advancements in the coupling of wave and surge models. This coupling has been implemented typically with heterogeneous meshes, which is disadvantageous because it requires intra-model interpolation at the boundaries of the nested, structured wave meshes and inter-model interpolation between the wave and circulation meshes. The recent introduction of unstructured wave models makes nesting unnecessary. The unstructured-mesh SWAN wave and ADCIRC circulation models are coupled in this work so that they run on the same unstructured mesh. This identical, homogeneous mesh allows the physics of wave-circulation interactions to be resolved correctly in both models. The unstructured mesh can be applied on a large domain to follow seamlessly all energy from deep to shallow water. There is no nesting or overlapping of structured wave meshes, and there is no inter-model interpolation. Variables and forces reside at identical, vertex-based locations. Information can be passed without interpolation, thus reducing significantly the communication costs.
The coupled SWAN+ADCIRC model is highly scalable and integrates seamlessly the physics and numerics from deep ocean to shelf to floodplain. Waves, water levels and currents are allowed to interact in complex problems and in a way that is accurate and efficient to thousands of computational cores. The coupled model is validated against extensive measurements of waves and surge during the four recent Gulf hurricanes. Furthermore, the coupling paradigm employed by SWAN+ADCIRC does not interfere with the already-excellent scalability of the component models, and the coupled model maintains its scalability to 7,168 computational cores. SWAN+ADCIRC is well-suited for the simulation of hurricane waves and surge.