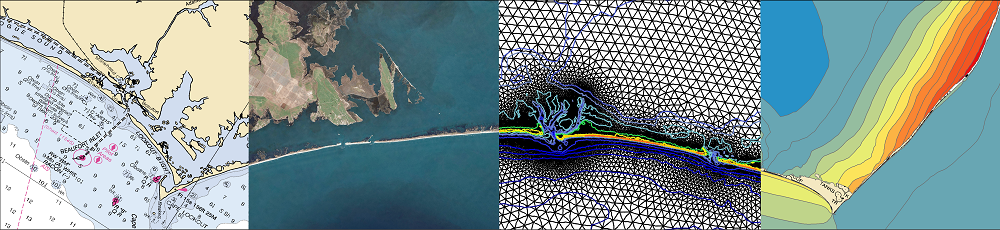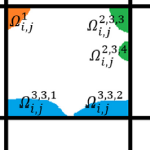
Subgrid modeling to account for unresolved topography within the context of shallow water equations relies on the use of coarse grids for computational efficiency. However, excessively coarse grids can lead to artificial cross flows between hydrologically disconnected areas separated by physical barriers smaller than the grid size. An approach based on introducing cell and edge clones, consisting of connected groups of pixels in each cell, is able to systematically remove such artificial cross flows. Such an approach considers that the subgrid barriers permanently divide flow among clones and effectively restrict flow to a predetermined path. In this work, a simple algorithm, along with the use of an overtopping formula, is proposed to extend the clone approach to a scenario in which clones are allowed to be further split and merged as needed, depending on the surface elevation during a given runtime. The algorithm is intended for accommodating the possibility of the subgrid barriers being inundated and no-longer dividing the flow during an extreme event. The performance of the proposed algorithm is demonstrated through a series of idealized and more realistic test cases, showing considerable improvements over existing methodologies.
A Begmohammadi, D Wirasaet, Z Silver, D Bolster, AB Kennedy, JC Dietrich (2021). “Subgrid surface connectivity for storm surge modeling.” Advances in Water Resources, 153, 103939, DOI: 10.1016/j.advwatres.2021.103939.
