A number of finite-element based shallow water models use the GWC (generalized wave continuity) algorithm, first introduced by Lynch and Gray in 1979, to suppress short wave noise without artificial or numerical damping. Nearly all of these, including the ADCIRC (ADvanced 3D CIRCulation model developed by Westerink and Luettich) model used in our research, utilize the non-conservative form of the momentum equation to obtain the velocity field. However, as early as 1990, it was discovered that the inconsistent treatment of the advective terms between the GWC equation (which uses the conservative form of the momentum equation in its formulation) and the non-conservative momentum (NCM) equation was causing instabilities. Additional analyses by Kinnmark and Aldama, among others, provided further evidence that the conservative form of the momentum (CM) equation may improve accuracy and stability, particularly for simulations that have regions of highly advective flows, e.g., converging flow near inlets and around barrier islands. Furthermore, as the ADCIRC modeling group begins to explore alternative algorithms for the continuity equations (e.g., discontinuous Galerkin algorithm instead of GWC), the conservative form of the momentum equation would facilitate model coupling. For these reasons, we modified the ADCIRC code to use the conservative form of the momentum equation. The impact of this change on mass balance, stability, and accuracy (spatial and temporal) is rigorously assessed, first for ID barotropic flows and later for 2D barotropic flows in a variety of basins. Results from the 1D experiments indicate the following: global mass balance improves up to two orders of magnitude, depending on the domain; local mass balance greatly improves in areas where steep bathymetry gradients occur; when combined with a predictor-corrector time-marching algorithm, stability increases by at least a factor of two (for a given level of mass balance error); and the form of the momentum equation does not cause a significant change in temporal or spatial accuracy when evaluating the two different time-marching algorithms.
KM Dresback, RL Kolar, JC Dietrich (2002). “Impact of the Form of the Momentum Equation on Shallow Water Models based on the Generalized Wave Continuity Equation.” Proceedings of the XIV International Conference on Computational Methods in Water Resources (CMWR), SM Hassanizadeh, RJ Schotting, WG Gray, and GF Pinder, eds., 47, 1573-1580.
Hydrodynamic models are used for a variety of purposes, such as the modeling of hurricane storm surges, the study of tidal circulation patterns, and the planning of naval fleet operations. One such hydrodynamic model is ADCIRC (ADvanced CIRCulation), which was developed more than 20 years ago and has been refined continuously by researchers across North America. ADCIRC is based on the shallow water equations and includes many of the features necessary to model complex hydrodynamic systems. However, some of these features were implemented in an attempt to solve specific problems, and their behaviors were never rigorously assessed. For instance, the model uses a wetting and drying algorithm to simulate the ebb and flow of tides in coastal regions. This behavior is important in many applications, and it must be modeled correctly. This research thesis will: (1) refute an attack on the usefulness of the finite volume method for computing mass balance errors, (2) lay the groundwork for a future study that will automate the placement of grid points based on a minimization of local mass balance error, (3) implement and assess the wetting and drying algorithm in one-, two-, and three-dimensional versions of the ADCIRC model, (4) identify a set of optimal parameters for wetting and drying simulations, (5) prove that recent updates to the wetting and drying algorithm were beneficial, and (6) show that smaller mass balance errors are obtained when they are computed for each vertical element in the water column.
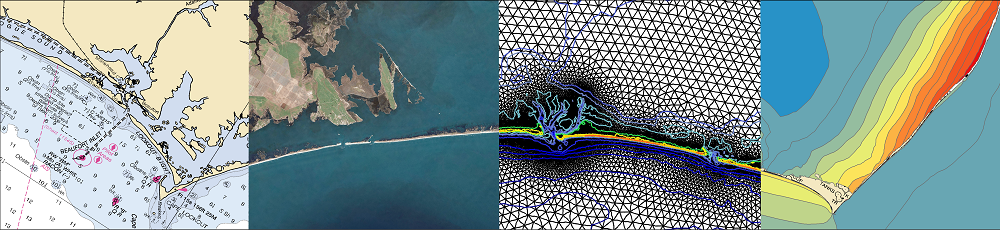
Nearly all generalized wave continuity (GWC)-based models utilize the velocity-based, non-conservative form of the momentum equation to obtain the depth-averaged changes in velocity. It has been hypothesized that a flux-based, conservative form of the momentum equation may improve accuracy and stability. Herein, we study the impact of the choice of dependent variable and form of the momentum equation in a GWC-based finite element shallow water model. The impact of this change on mass balance, stability, and accuracy (spatial and temporal) is rigorously assessed, first for 1D barotropic flows and then for 2D barotropic flows in a variety of basins. Both 1D and 2D results indicate that the conservative form improves mass balance on both global and local scales, with the most significant gains found in local mass balance in areas with steep bathymetry gradients. This is also the region where the conservative form shows an increase in local spatial accuracy. Taylor series analysis and numerical simulations indicate a strong correlation between local spatial truncation errors and local mass balance errors. Stability, temporal accuracy and global spatial accuracy do not show statistically significant changes between the two algorithms in both 1D and 2D studies.
The ADvanced CIRCulation (ADCIRC) model is a finite-element hydrodynamic model based on the generalized wave continuity equation (GWCE). The model assumed fixed land boundaries until a wetting and drying algorithm was implemented by Luettich and Westerink in 1995. The algorithm uses an element-based approach, effectively turning elements on and off based on water depths and a water level gradient. While robust in some simulations, the algorithm can be subject to instabilities in the solution during highly nonlinear events. Thus, a rigorous assessment of the algorithm’s stability, accuracy, mass balance properties, and parameter sensitivity under a variety of conditions is needed. Herein, we examine these issues using a one-dimensional implementation of the wetting and drying algorithm for basins with a linear slope; future studies will examine a wider variety of real and idealized basins. We believe the results of this work will benefit similar studies in two- or three-dimensions, for users and developers of both ADCIRC and other finite element models.
This paper builds upon earlier work that developed and evaluated a 1D predictor-corrector time-marching algorithm for wave equation models and extends it to 2D. Typically, the generalized wave continuity equation (GWCE) utilizes a three time-level semi-implicit scheme centred at k, and the momentum equation uses a two time-level scheme centred at k + 1/2. It has been shown that in highly non-linear applications, the algorithm becomes unstable at even moderate Courant numbers. This work implements and analyses an implicit treatment of the non-linear terms through the use of an iterative time-marching algorithm in the two-dimensional framework. Stability results show at least an eight-fold increase in the maximum time step, depending on the domain. Studies also examined the sensitivity of the G parameter (a numerical weighting parameter in the GWCE) with results showing the greatest increase in stability occurs when 1 <= G/Tmax <= 10, a range that coincides with the recommended range to minimize errors. Convergence studies indicate an increase in temporal accuracy from first order to second order, while overall error is less than the original algorithm, even at higher time steps. Finally, a parallel implementation of the new algorithm shows that it scales well.