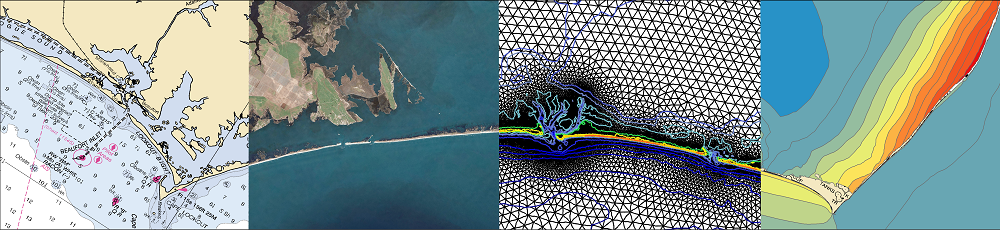
Mass balance error has been computed traditionally by using conventional fluxes derived from the conservation of mass equation, but recent literature supports a method based on fluxes that are consistent with the discretization of the governing equations. By comparing the mass residuals from these two methods to the truncation errors produced by the discretization of the governing equations, we show that the conventional fluxes produce mass residuals that are more descriptive of the overall behavior of the model, i.e., they are better correlated with truncation error. Then we demonstrate that these mass residuals can be used as a criterion for mesh refinement. In an example using a one-dimensional shallow water model, we demonstrate that, by moving nodes from regions with large mass residuals to regions with small mass residuals, a mesh can be developed that shows less truncation error than a mesh developed by using localized truncation error analysis. And, in an example using a two-dimensional shallow water model, we demonstrate that the computed solution can be improved in regions with large mass residuals through mesh refinement.
