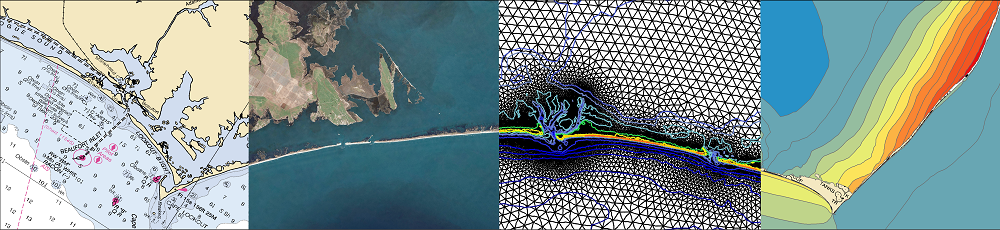
On large geographic scales, ocean waves are represented in a spectral sense via the action balance equation, which propagates action density through both geographic and spectral space. In this paper, a new computational spectral wave model is developed by using discontinuous Galerkin (DG) methods in both geographic and spectral space. DG methods allow for the use of unstructured geographic meshes and higher-order approximations for action propagation in both geographic and spectral space, which we show leads to increased accuracy. This DG spectral wave propagation model is verified and validated through comparisons to manufactured and analytic solutions as well as to the Simulating WAves Nearshore (SWAN) model. Coupled wave/circulation models are needed for many applications including for the interaction between waves and currents during daily wind and tide driven flows. We loosely couple the newDGspectralwavemodel to the DG Shallow Water Equation Model (DG-SWEM), an existing DG circulation model. In addition to formulating the DG method for the coupled wave/circulation model, we derive an a priori error estimate. Preliminary numerical results of the DG coupled wave/circulation model are presented with comparisons to DG-SWEM coupled tightly to SWAN.
JD Meixner, JC Dietrich, CN Dawson, M Zijlema, LH Holthuijsen (2014). “A Discontinuous Galerkin Coupled Wave Propagation/Circulation Model.” Journal of Scientific Computing, 59, 334–370, DOI: 10.1007/s10915-013-9761-5.
