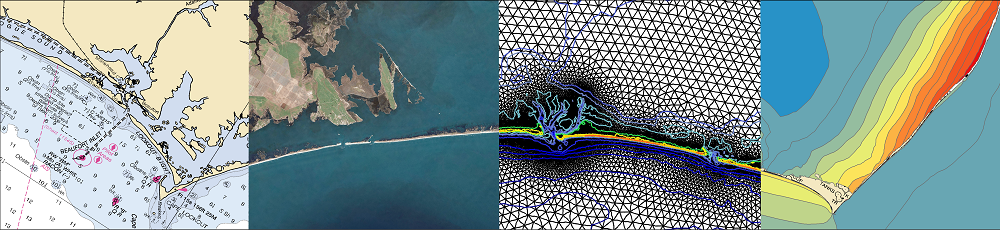
This paper builds upon earlier work that developed and evaluated a 1D predictor-corrector time-marching algorithm for wave equation models and extends it to 2D. Typically, the generalized wave continuity equation (GWCE) utilizes a three time-level semi-implicit scheme centred at k, and the momentum equation uses a two time-level scheme centred at k + 1/2. It has been shown that in highly non-linear applications, the algorithm becomes unstable at even moderate Courant numbers. This work implements and analyses an implicit treatment of the non-linear terms through the use of an iterative time-marching algorithm in the two-dimensional framework. Stability results show at least an eight-fold increase in the maximum time step, depending on the domain. Studies also examined the sensitivity of the G parameter (a numerical weighting parameter in the GWCE) with results showing the greatest increase in stability occurs when 1 <= G/Tmax <= 10, a range that coincides with the recommended range to minimize errors. Convergence studies indicate an increase in temporal accuracy from first order to second order, while overall error is less than the original algorithm, even at higher time steps. Finally, a parallel implementation of the new algorithm shows that it scales well.
KM Dresback, RL Kolar, JC Dietrich (2004). “A 2D Implicit Time-Marching Algorithm for Shallow Water Models Based on the Generalized Wave Continuity Equation.” International Journal for Numerical Methods in Fluids, 45(3), 253-274.
