A large, unpredicted, water level increase appeared along a substantial section of the western Louisiana and northern Texas (LATEX) coasts 12-24 hrs in advance of the landfall of Hurricane Ike (2008), with water levels in some areas reaching 3m above mean sea level. During this time the cyclonic wind field was largely shore parallel throughout the region. A similar early water level rise was reported for both the 1900 and the 1915 Galveston Hurricanes. The Ike forerunner anomaly occurred over a much larger area and prior to the primary coastal surge which was driven by onshore directed winds to the right of the storm track. We diagnose the forerunner surge as being generated by Ekman setup on the wide and shallow LATEX shelf. The longer forerunner time scale additionally served to increase water levels significantly in narrow-entranced coastal bays. The forerunner surge generated a freely propagating continental shelf wave with greater than 1.4m peak elevation that travelled coherently along the coast to Southern Texas, and was 300km in advance of the storm track at the time of landfall. This was, at some locations, the largest water level increase seen throughout the storm, and appears to be the largest freely-propagating shelf wave ever reported. Ekman setup-driven forerunners will be most significant on wide, shallow shelves subject to large wind fields, and need to be considered for planning and forecasting in these cases.
AB Kennedy, U Gravois, BC Zachry, JJ Westerink, ME Hope, JC Dietrich, MD Powell, AT Cox, RA Luettich Jr, RG Dean (2011). “Origin of the Hurricane Ike Forerunner Surge.” Geophysical Research Letters, 38, L08608, doi:10.1029/2011GL047090.
The unstructured-mesh SWAN spectral wave model and the ADCIRC shallow-water circulation model have been integrated into a tightly-coupled SWAN+ADCIRC model. The model components are applied to an identical, unstructured mesh; share parallel computing infrastructure; and run sequentially in time. Wind speeds, water levels, currents and radiation stress gradients are vertex-based, and therefore can be passed through memory or cache to each model component. Parallel simulations based on domain decomposition utilize identical sub-meshes, and the communication is highly localized. Inter-model communication is intra-core, while intra-model communication is inter-core but is local and efficient because it is solely on adjacent sub-mesh edges. The resulting integrated SWAN+ADCIRC system is highly scalable and allows for localized increases in resolution without the complexity or cost of nested meshes or global interpolation between heterogeneous meshes. Hurricane waves and storm surge are validated for Hurricanes Katrina and Rita, demonstrating the importance of inclusion of the wave-circulation interactions, and efficient performance is demonstrated to 3062 computational cores.
Hurricanes Katrina and Rita were powerful storms that impacted southern Louisiana and Mississippi during the 2005 hurricane season. In Part I, the authors describe and validate a high-resolution coupled riverine flow, tide, wind, wave, and storm surge model for this region. Herein, the model is used to examine the evolution of these hurricanes in more detail. Synoptic histories show how storm tracks, winds, and waves interacted with the topography, the protruding Mississippi River delta, east-west shorelines, man-made structures, and low-lying marshes to develop and propagate storm surge. Perturbations of the model, in which the waves were not included, show the proportional importance of the wave radiation stress gradient induced setup.
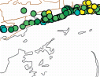
A coupled system of wind, wind wave, and coastal circulation models has been implemented for southern Louisiana and Mississippi to simulate riverine flows, tides, wind waves, and hurricane storm surge in the region. The system combines the NOAA Hurricane Research Division Wind Analysis System (H*WIND) and the Interactive Objective Kinematic Analysis (IOKA) kinematic wind analyses, the Wave Model (WAM) offshore and Steady-State Irregular Wave (STWAVE) nearshore wind wave models, and the Advanced Circulation (ADCIRC) basin to channel-scale unstructured grid circulation model. The system emphasizes a high-resolution (down to 50m) representation of the geometry, bathymetry, and topography; nonlinear coupling of all processes including wind wave radiation stress-induced set up; and objective specification of frictional parameters based on land-cover databases and commonly used parameters. Riverine flows and tides are validated for no storm conditions, while winds, wind waves, hydrographs, and high water marks are validated for Hurricanes Katrina and Rita.
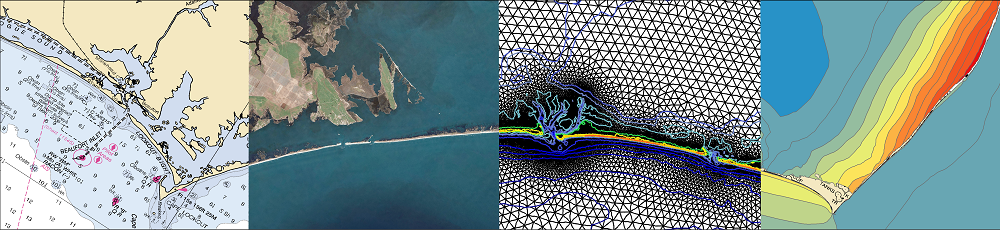
Hurricane Katrina caused devastating flooding in St. Bernard Parish, Louisiana. Storm surge surrounded the polder that comprises heavily populated sections of the Parish in addition to the Lower 9th Ward section of Orleans Parish. Surge propagated along several pathways to reach levees and walls around the polder’s periphery. Extreme water levels led to breaches in the levee/wall system which, along with wave overtopping and steady overflow, led to considerable flood water entering the polder. Generation and evolution of the storm surge as it propagated into the region is examined using results from the SL15 regional application of the ADCIRC storm surge model. Fluxes of water into the region through navigation channels are compared to fluxes which entered through Lake Borgne and over inundated wetlands surrounding the lake. Fluxes through Lake Borgne and adjacent wetlands were found to be the predominant source of water reaching the region. Various sources of flood water along the polder periphery are examined. Flood water primarily entered through the east and west sides of the polder. Different peak surges and hydrograph shapes were experienced along the polder boundaries, and reasons for the spatial variability in surge conditions are discussed.
Mass balance error has been computed traditionally by using conventional fluxes derived from the conservation of mass equation, but recent literature supports a method based on fluxes that are consistent with the discretization of the governing equations. By comparing the mass residuals from these two methods to the truncation errors produced by the discretization of the governing equations, we show that the conventional fluxes produce mass residuals that are more descriptive of the overall behavior of the model, i.e., they are better correlated with truncation error. Then we demonstrate that these mass residuals can be used as a criterion for mesh refinement. In an example using a one-dimensional shallow water model, we demonstrate that, by moving nodes from regions with large mass residuals to regions with small mass residuals, a mesh can be developed that shows less truncation error than a mesh developed by using localized truncation error analysis. And, in an example using a two-dimensional shallow water model, we demonstrate that the computed solution can be improved in regions with large mass residuals through mesh refinement.
Nearly all generalized wave continuity (GWC)-based models utilize the velocity-based, non-conservative form of the momentum equation to obtain the depth-averaged changes in velocity. It has been hypothesized that a flux-based, conservative form of the momentum equation may improve accuracy and stability. Herein, we study the impact of the choice of dependent variable and form of the momentum equation in a GWC-based finite element shallow water model. The impact of this change on mass balance, stability, and accuracy (spatial and temporal) is rigorously assessed, first for 1D barotropic flows and then for 2D barotropic flows in a variety of basins. Both 1D and 2D results indicate that the conservative form improves mass balance on both global and local scales, with the most significant gains found in local mass balance in areas with steep bathymetry gradients. This is also the region where the conservative form shows an increase in local spatial accuracy. Taylor series analysis and numerical simulations indicate a strong correlation between local spatial truncation errors and local mass balance errors. Stability, temporal accuracy and global spatial accuracy do not show statistically significant changes between the two algorithms in both 1D and 2D studies.
This paper builds upon earlier work that developed and evaluated a 1D predictor-corrector time-marching algorithm for wave equation models and extends it to 2D. Typically, the generalized wave continuity equation (GWCE) utilizes a three time-level semi-implicit scheme centred at k, and the momentum equation uses a two time-level scheme centred at k + 1/2. It has been shown that in highly non-linear applications, the algorithm becomes unstable at even moderate Courant numbers. This work implements and analyses an implicit treatment of the non-linear terms through the use of an iterative time-marching algorithm in the two-dimensional framework. Stability results show at least an eight-fold increase in the maximum time step, depending on the domain. Studies also examined the sensitivity of the G parameter (a numerical weighting parameter in the GWCE) with results showing the greatest increase in stability occurs when 1 <= G/Tmax <= 10, a range that coincides with the recommended range to minimize errors. Convergence studies indicate an increase in temporal accuracy from first order to second order, while overall error is less than the original algorithm, even at higher time steps. Finally, a parallel implementation of the new algorithm shows that it scales well.